An Introduction to Ion-Optics

Page
3

for beam lines with paraxial beams

Code: COSY Infinity:

(x, a, y, b, l, dK, dm, dz)

Needed for complex ion-optical systems including several

charge states

different masses

velocities (e.g. Wien Filter)

higher order corrections

Not defined in the figure are:

dK = dK/K = rel. energy

dm = dm/m = rel. energy

dz = dq/q = rel. charge change

a = px/p0

b = py/p0

All parameters are relative

to “central ray” properties

Not defined in the figure are:

dp/p = rel. momentum

l = beam pulse length

All parameters are relative

to “central ray”

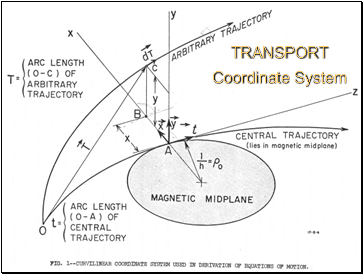
central ray

Note: Notations in the Literature is not consistent! Sorry, neither will I be.

Slide 11

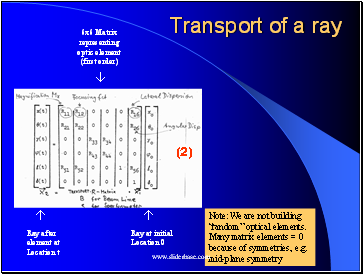
Ray at initial

Location 1





TRANSPORT Coordinate System

Slide 12

Transport of a ray

Ray at initial

Location 0

Ray after element at

Location t





6x6 Matrix

representing

optic element

(first order)



Note: We are not building “random” optical elements.

Many matrix elements = 0

because of symmetries, e.g. mid-plane symmetry

(2)

Slide 13

TRANSPORT matrices of a Drift and a Quadrupole

For reference of TRANSPORT code and formalism:

K.L. Brown, F. Rothacker, D.C. Carey, and Ch. Iselin,

TRANSPORT: A computer program for designing

charged particle beam transport systems, SLAC-91,

Rev. 2, UC-28 (I/A), also: CERN 80-04 Super Proton

Synchrotron Division, 18 March 1980, Geneva,

Manual plus Appendices available on Webpage:

ftp://ftp.psi.ch/psi/transport.beam/CERN-80-04/

David. C. Carey, The optics of Charged Particle Beams,

1987, Hardwood Academic Publ. GmbH, Chur Switzerland

Slide 14

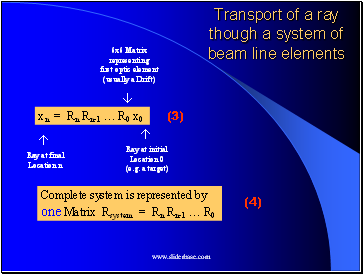
Transport of a ray though a system of beam line elements

Ray at initial

Location 0

(e.g. a target)

Ray at final

Location n





6x6 Matrix

representing

first optic element

(usually a Drift)



xn = Rn Rn-1 … R0 x0

Complete system is represented by

one Matrix Rsystem = Rn Rn-1 … R0

(3)

(4)

Slide 15

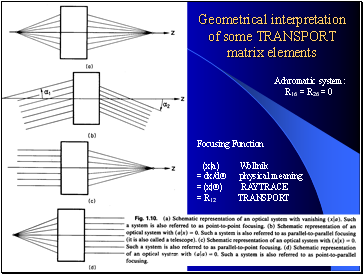
Geometrical interpretation of some TRANSPORT matrix elements

Wollnik, p. 16

Focusing Function

(x|a) Wollnik

= dx/dQ physical meaning

= (x|Q) RAYTRACE

= R12 TRANSPORT

Achromatic system:

R16 = R26 = 0

Slide 16

Defining a BEAM