Atomic Structure and Periodicity

Page
1

Slide 1

Chapter 7 Atomic Structure and Periodicity

Electromagnetic Radiation

Radiant energy that exhibits wavelength-like behavior and travels through space at the speed of light in a vacuum.

Example: The sun light, energy used in microwave oven, the x-rays used by doctors.

Slide 2

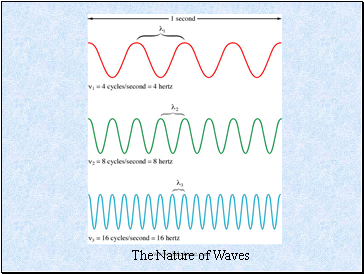
Waves

Waves have 3 primary characteristics:

1. Wavelength (): distance between two consecutive peaks in a wave.

2. Frequency (): number of waves (cycles) per second that pass a given point in space.

3. Speed: speed of light is 2.9979  108 m/s. We will use 3.00 x108 m/s.

Slide 3

The Nature of Waves

Slide 4

Wavelength and frequency can be interconverted and they have an inverse relationship

 = c/

 = frequency (s1)

 = wavelength (m)

c = speed of light (m s1)

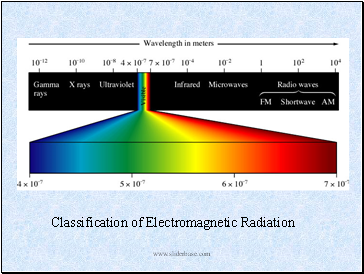
Wavelength is also given in nm (1 nm = 10-9 m) and Angstroms (Å) (1 Å = 10-10 m).

The frequency value of s1 or 1/s is also called “hertz (Hz)” like KHz on the radio.

Slide 5

Classification of Electromagnetic Radiation

Slide 6

Example: When green light is emitted from an oxygen atom it has a wavelength of 558 nm. What is the frequency?

We know,

 = c/ where, c = speed of light

= 3.00 x 108m/s

 = wavelength

= 558 nm

(need to convert in m)

Slide 7

Planck’s Constant

Transfer of energy is quantized, and can only occur in discrete units, called quanta.

E = change in energy, in J

h = Planck’s constant, 6.626  1034 J s

 = frequency, in s1

 = wavelength, in m

Slide 8

Example: The Blue color in fireworks is often achieved by heating copper (I) chloride (CuCl) to about 1200oC. Then the compound emits blue light having a wavelength of 450 nm. What is the increment of energy (the quantum) that is emitted at 4.50 x 102 nm by CuCl?

The quantum of energy can be calculate from the equation

E = h

The frequency  for this case can be calculated as follows:

So,

E = h = (6.626 x 10-34J.s)(6.66 x 1014 s-1)

= 4.41 x 10-19J