Gravity and Circular Motion Revision

Page
2

Gravitational field

A gravitational field is an area of space subject to the force of gravity. Due to the inverse square law relationship, the strength of the field fades quickly with distance.

The field strength is defined as

The force per unit mass OR

g = F/m in Nkg-1

Slide 15

Radial Field

Planets and other spherical objects exhibit radial fields, that is the field fades along the radius extending into space from the centre of the planet according to the equation

g = -GM/r2

Where M is

the mass of the planet

Slide 16

Gravitational Potential

Potential is a measure of the energy in the field at a point compared to an infinite distance away.

The zero of potential is defined at

Infinity

Potential at a point is

the work done to move unit mass from infinity to that point. It has a negative value.

The equation for potential in a radial field is

V = -GM/r

Slide 17

Potential Gradient

In stronger gravitational fields, the potential graph is steeper. The potential gradient is

ΔV/Δr

And the field strength g is

equal to the magnitude of the Potential gradient

g = -ΔV/Δr

Slide 18

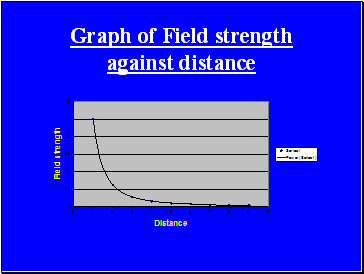
Graph of Field strength against distance

Slide 19

Field strength graph notes

Outside the planet field strength

follows an inverse square law

Inside the planet field strength

fades linearly to zero at the centre of gravity

Field strength is always

positive

Slide 20

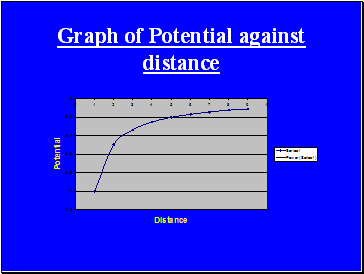
Graph of Potential against distance

Slide 21

Potential Graph Notes

Potential is always

negative

Potential has zero value at

infinity

Compared to Field strength graph,

Potential graph is less steep

Slide 22

Orbits

Circular orbits follow the simple rules of gravitation and circular motion. We can put the force equations equal to each other.

F = mv2/r = -Gm1m2/r2

So we can calculate v

v2 = -Gm1/r

Slide 23

More orbital mechanics

Period T is the time for a complete orbit, a year. It is given by the formula.