Atomic Structure

Page
3

Slide 12

Quantization of Angular Momentum

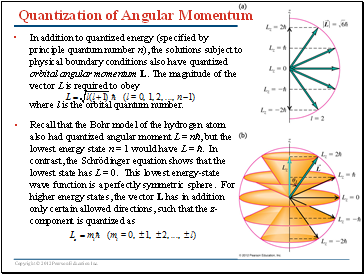
In addition to quantized energy (specified by principle quantum number n), the solutions subject to physical boundary conditions also have quantized orbital angular momentum L. The magnitude of the vector L is required to obey

where l is the orbital quantum number.

Recall that the Bohr model of the hydrogen atom also had quantized angular moment L = nħ, but the lowest energy state n = 1 would have L = ħ. In contrast, the Schrödinger equation shows that the lowest state has L = 0. This lowest energy-state wave function is a perfectly symmetric sphere. For higher energy states, the vector L has in addition only certain allowed directions, such that the z-component is quantized as

Slide 13

The hydrogen atom: Degeneracy

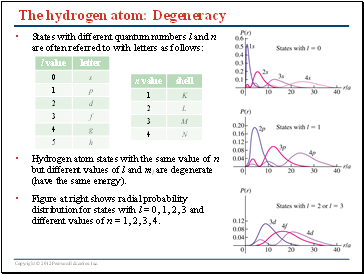
States with different quantum numbers l and n are often referred to with letters as follows:

Hydrogen atom states with the same value of n but different values of l and ml are degenerate (have the same energy).

Figure at right shows radial probability distribution for states with l = 0, 1, 2, 3 and different values of n = 1, 2, 3, 4.

Slide 14

The hydrogen atom: Quantum states

Table 41.1 (below) summarizes the quantum states of the hydrogen atom. For each value of the quantum number n, there are n possible values of the quantum number l. For each value of l, there are 2l + 1 values of the quantum number ml.

Example 41.2: How many distinct states of the hydrogen atom (n, l, ml) are there for the n = 3 state? What are their energies?

The n = 3 state has possible l values 0, 1, or 2. Each l value has ml possible values of (0), (-1, 0, 1), or (-2, -1, 0, 1, 2). The total number of states is then 1 + 3 + 5 = 9. We will see later that there is another quantum number s, for electron spin (±½), so there are actually 18 possible states for n = 3.

Each of these states have the same n, so they all have the same energy.

Slide 15

The hydrogen atom: Probability distributions I

States of the hydrogen atom with l = 0 (zero orbital angular momentum) have spherically symmetric wave functions that depend on r but not on  or . These are called s states. Figure 41.9 (below) shows the electron probability distributions for three of these states.

Follow Example 41.4.

Slide 16

The hydrogen atom: Probability distributions II

States of the hydrogen atom with nonzero orbital angular momentum, such as p states (l = 1) and d states (l = 2), have wave functions that are not spherically symmetric. Figure 41.10 (below) shows the electron probability distributions for several of these states, as well as for two spherically symmetric s states.