Optical Illusions

Page
4

constraint line: on which the optical flow vector lies

Slide 17

Errors in Movement: How image movement is estimated

Second stage

Combination of the motion components from differently oriented edges within a small patch

Estimate the optical flow vector closest to all the constraint lines

The minimum squared distance from the lines

Over-determined system

Solution is biased

Does not correspond to the actual flow

Depends on the features in the patch, texture

Slide 18

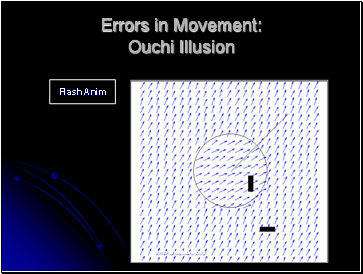
Errors in Movement: Ouchi Illusion

Estimated flows of surrounding area and inset area are different

Smaller in length than the actual flow and it is closer in direction to the majority of normal flow vectors in a region

Slide 19

Errors in Movement: Ouchi Illusion

Flash Anim

Slide 20

Errors in Movement: Wheels Illusion

Every point on the image moves on a straight line through the image center

Actual flow vectors are moving radially from the image center outwards, otherwise they are moving inwards

Slide 21

Errors in Movement: Wheels Illusion

Slide 22

Errors in Movement: Wheels Illusion

Slide 23

Errors in Movement: Wheels Illusion

Slide 24

Errors in Movement: Spiral Illusion

Spiral rotation around its center

Not circular

Contract or expand

Counter-clockwise

Red: actualmotion vector

Blue: normal flow vectors

Slide 25

Errors in Movement: Moving sinusoids

Smooth curves may be perceived to deform non-rigidly when translated in the image plane

Low amplitude: appears to deform non-rigidly

High amplitude: perceived as the true translation

Flash Anim

Slide 26

Shape from Motion: The Constraint

A biased estimate for the surface normal

Motion parameters

Orientation of the image lines (that is the texture of the plane)

As a parameterization for the surface normal

Slant (σ)

The angle between N and the negative optical axis

Tilt (τ)

The angle between the parallel projection of N on the image plane and the image x-axis.