Sound

Page
12

Slide 48

Sound Level in Decibels

The greater the intensity of a sound at a certain place, the louder it will sound. But doubling the intensity will not make it seem twice as loud. Experiments show that the intensity must increase by about a factor of 10 before the sound will seem twice as loud to us. A sound with a 100 times greater intensity will sound about 4 times louder. Therefore, we measure sound level (loudness) based on a logarithic scale. The sound level in decibels (dB) is given by:

Ex: At a certain distance from a siren, the intensity of the sound waves might be 10 –5 W / m 2 . The sound level at this location would be:

Note: According to this definition, a sound at the intensity level registers zero decibels:

(in decibels)

10 log (10 –5 / 10 –12) = 10 log (10 7 ) = 70 dB

10 log (10 –12 / 10 –12) = 10 log (1 ) = 0 dB

Slide 49

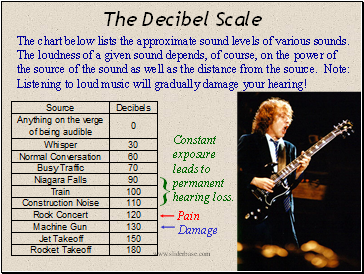
The Decibel Scale

Pain

Damage

}

Constant exposure leads to permanent hearing loss.

The chart below lists the approximate sound levels of various sounds. The loudness of a given sound depends, of course, on the power of the source of the sound as well as the distance from the source. Note: Listening to loud music will gradually damage your hearing!

Slide 50

Intensity & Sound Level

Every time the intensity of a sound is increased by a factor of 10, the sound level goes up by 10 dB (and the sound seems to us to be about twice as loud). Let’s compare a 90 dB shout to a 30 dB whisper. The shout is 60 dB louder, which means its intensity is 10 to the 6th power (a million) times greater. Proof:

60 = 1 - 2 = 10 log (I 1 / I 0 ) - 10 log(I 2 / I 0 ) = 10 log

60 = 10 log (I 1 / I 2 )

6 = log (I 1 / I 2 )

10 6 = I 1 / I 2

Compare intensities: 80 dB vs. 60 dB

Compare intensities: 100 dB vs. 75 dB

Compare sound levels: 4.2 · 10 –4 W / m 2 vs. 4.2 · 10 –7 W / m 2

answers:

factor of 100

factor of 316 (10 2.5 = 316)

differ by 30 dB ( I’s differ by 3 powers of 10 )

Slide 51

Decibel Example

Suppose a 75 g egg is dropped from 50 m up onto the sidewalk. The splat takes 0.05 s. Nearly all of the gravitational potential energy the egg had originally is converted into thermal energy, but a very small fraction goes into sound energy. Let’s say this fraction is only 6.7582 · 10 –11. How loud is the splat heard from the point at which the egg was dropped? Hints: Answers:

How much energy does the egg originally have?

How much of that energy goes into sound?

Calculate sound power output of the egg.

Figure intensity at 50 m up. (Assume the hemispherical wavefronts.)