Atomic Structure and Periodic Trends

Page
17

Y(2,1) =y(2)y(1) s(2,1)

exchange

Slide 144

But in the spin wave functions s(2,1)?

s(1,2) = a(1)a(2) s(1,2) = b(1)b(2)

s(1,2) = 1/2[a(1)b(2) - b(1)a(2)] s(1,2) = 1/2[a(1)b(2) +b(1)a(2)]

+

-

Slide 145

But in the spin wave functions s(2,1)?

s(1,2) = a(1)a(2) = a(2)a(1) = s(2,1) s(1,2) = b(1)b(2) = b(2)b(1) = s(2,1)

s(1,2) = 1/2[a(1)b(2) - b(1)a(2)]

1/2[a(2)b(1) - b(2)a(1)]

- 1/2[b(2)a(1) - a(2)b(1)]

- 1/2[a(1)b(2) - b(1)a(2)] = - s(2,1)

ex

ex

ex

antisymmetric

symmetric

symmetric

Slide 146

In analogy:

s(1,2) = 1/2[a(1)b(2) + b(1)a(2)]

1/2[a(2)b(1) + b(2)a(1)]

+ 1/2[b(2)a(1) + a(2)b(1)]

+ 1/2[a(1)b(2) + b(1)a(2)] = + s(2,1)

+

ex

symmetric

Slide 147

Hence, the only allowed overall wavefunction is:

With an antiparallel arrangement of spins

Y(1,2) =y(1)y(2) [a(1)b(2) - b(1)a(2)]/2

Slide 148

5) Slater’s Rules

Approximate method for estimating the effective nuclear charge

Zeff = Z - S

Where Z is the actual nuclear charge and S is a shielding constant.

Slide 149

Computing S

1. Divide orbitals into groups

(1s) (2s2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f)

Note s and p with same n grouped together

2. There is no contribution to S from electron to the right of the one being considered.

3. A contribution is added to S for each electron in the same group as the one being considered – except in the (1s) group where the contribution is 0.30.

3. If the electron being considered is in an ns or np orbital, the electrons in the next lowest shell (n-1) each contribute 0.85 to S. Those electrons in lower shells ((n-2) and lower) contribute 1.00 to S.

4. If the electron being considered is an nd or nf orbital, all electrons below it in energy contribute 1.00 to S.

Slide 150

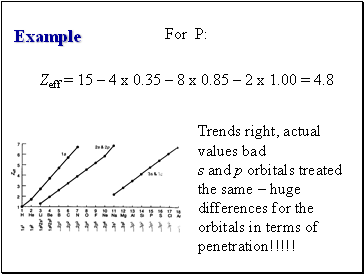
Example

For P:

Zeff = 15 – 4 x 0.35 – 8 x 0.85 – 2 x 1.00 = 4.8

Trends right, actual values bad

s and p orbitals treated the same – huge differences for the orbitals in terms of penetration!!!!!