Atomic Structure and Periodic Trends

Page
4

n = 1, 2, 3, 4, .

l = 0, 1, 2, 3, (n-1)

ml = -l, -l+1, -l+2, 0, ., l-1, l

Important

Slide 29

You are familiar with these .

n is the integer number associated with an orbital

Different l values have different names arising from early spectroscopy

e.g., l =0 is labelled

l =1 is labelled

l =2 is labelled

l =3 is labelled etc .

Important

Slide 30

Looked at another way .

n =1 l=0 ml=0 1s orbital (1 of)

n =2 l=0 ml=0 2s orbital (1 of)

l=1 ml=-1, 0, 1 2p orbitals (3 of)

n =3 l=0 ml=0 3s orbital (1 of)

l=1 ml=-1, 0, 1 3p orbitals (3 of)

l=2 ml=-2,-1,0,1,2 3d orbitals (5 of)

etc. etc. etc.

Hence we begin to see the structure behind the periodic table emerge.

Important

Slide 31

Exercise 1;

Work out, and name, all the possible

orbitals with principal

quantum number n=5.

How many orbitals have n=5?

Slide 32

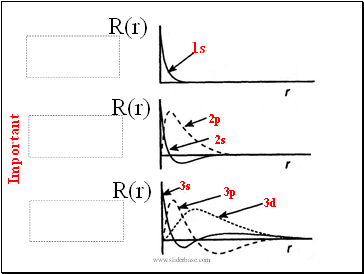
The Radial Wavefunctions

The radial wavefunctions for H-atom are the set of Laguerre functions in terms of n, l

a0 (=0.05292nm)

is the

-the most probable

orbital radius of an H-atom 1s electron.

Slide 33

R(r)

1s

2s

2p

3s

3p

3d

Important

R(r)

R(r)

Slide 34

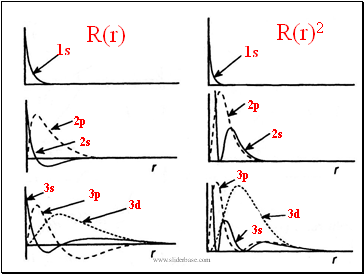
Revisit: The Born Interpretation

The square of the wavefunction,

at a point is proportional to the

of finding the particle at that point.

Y* = Y

In 1D: If the amplitude of the wavefunction of a particle at some point x is Y(x) then the probability of finding the particle between x and x +dx is proportional to

(x)Y*(x)dx = (x)

Y* is the complex conjugate of Y.

2

2

dx

Slide 35

R(r)2

R(r)

1s

2s

2p

3s

3d

1s

2s

2p

3s

3p

3d

3p

Slide 36

Radial Wavefunctions and the Born Interpretation

Slide 37

At long distances from the nucleus, all wavefunctions decay to .

Some wavefunctions are zero at the nucleus (namely, all but the l=0 (s) orbitals). For these orbitals, the electron has a zero probability of being found .

Some orbitals have nodes, ie, the wave function passes through zero; There are such radial nodes for each orbital.