Atomic Structure and Periodic Trends

Page
2

Consider 3 approaches:

Classical

Bohr Model (old quantum theory)

Full Quantum: Schrödinger Equation

Slide 10

Classically:

There is no theoretical restriction at all on v or r (there are infinitely many combinations with the same energy).

Hence the energy can take any value - it is

.

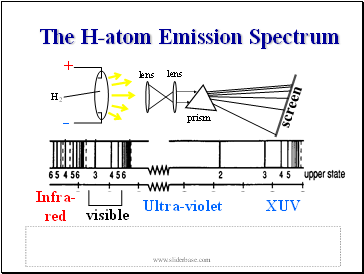
As a result transitions should be possible everywhere across the electromagnetic spectrum.

So lets see the spectrum .

Slide 11

The H-atom Emission Spectrum

Slide 12

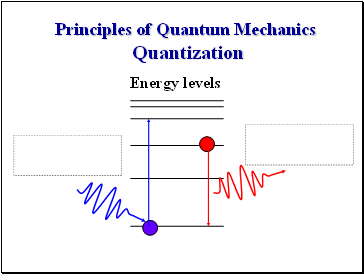
Principles of Quantum Mechanics Quantization

Energy levels

Slide 13

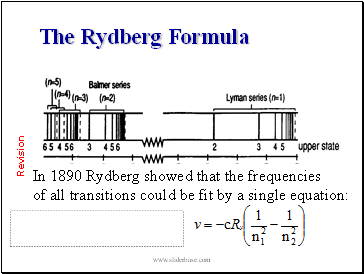
The Rydberg Formula

In 1890 Rydberg showed that the frequencies

of all transitions could be fit by a single equation:

Revision

Slide 14

Bohr Theory (old quantum)

Bohr explained the observed frequencies by restricting the allowed orbits the electron could occupy to particular circular orbits(by quantizing the angular momentum).

His theory gives energy levels:

Slide 15

The problem with Bohr Theory

Bohr theory works extremely well for the H-atom.

However;

it provides no explanation for the quantization of energy -it just happens to fit the observed spectrum

But, more seriously:

it just doesn’t work at all for any other atoms

Slide 16

Quantum mechanical Principles and the Solution of the Schrödinger Equation

Slide 17

Principles of Quantum Mechanics Quantization

Energy levels

Quantum mechanics

Classical mechanics

is continuous

Slide 18

Principles of Quantum Mechanics It’s all about probability

In classical mechanics

Position of object specified

In quantum mechanics

Only

of object at a particular location

Slide 19

Principles of Quantum Mechanics How do we describe the electrons in atoms?

You know: Electrons can be described as

(characterised by mass, momentum, position…)

p = h/l

De Broglie

e-

h = Planck’s constant = 6.626 10-34 Js

However: Electrons can also be described as

(characterised by wavelength, frequency, amplitude)