Atomic Structure and Periodic Trends

Page
5

Slide 38

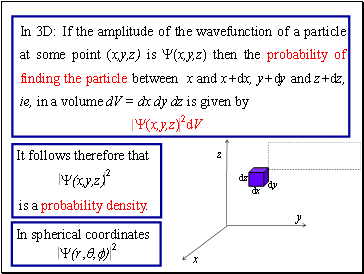
In 3D: If the amplitude of the wavefunction of a particle at some point (x,y,z) is Y(x,y,z) then the probability of finding the particle between x and x+dx, y+dy and z+dz, ie, in a volume dV = dx dy dz is given by

Y(x,y,z) dV

dx

dy

dz

x

z

y

It follows therefore that

2

2

Y(x,y,z)

is a probability density.

In spherical coordinates

2

Y(r,q,f)

Slide 39

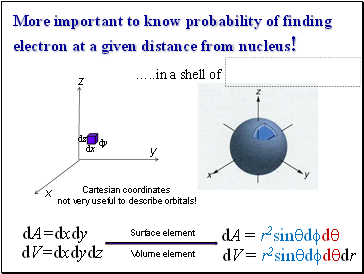
More important to know probability of finding electron at a given distance from nucleus!

dx

dy

dz

x

z

y

dV=dxdydz

Cartesian coordinates

not very useful to describe orbitals!

… in a shell of

dA = r2sinqdfdq

dA=dxdy

dV = r2sinqdfdqdr

Surface element

Volume element

Slide 40

The Surface area of a sphere is hence:

Slide 41

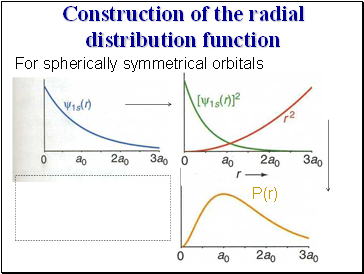
For spherically symmetric orbitals:

the radial distribution function is defined as

2

P(r)= 4pr2 Y(r)

and P(r)dr is the probability of finding the electron in a shell of radius r and thickness dr

Slide 42

Construction of the radial distribution function

For spherically symmetrical orbitals

P(r)

Slide 43

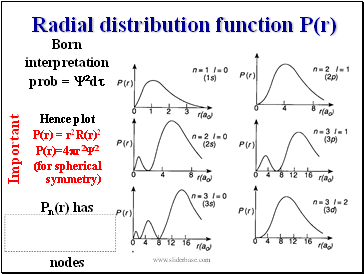
Radial distribution function P(r)

Important

Born

interpretation

prob = Y2dt

Hence plot

P(r) = r2R(r)2

P(r)=4pr2Y2

(for spherical symmetry)

Pn(r) has

nodes

Slide 44

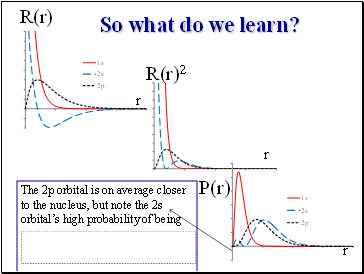
So what do we learn?

R(r)

R(r)2

P(r)

r

r

r

The 2p orbital is on average closer to the nucleus, but note the 2s orbital’s high probability of being

Slide 45

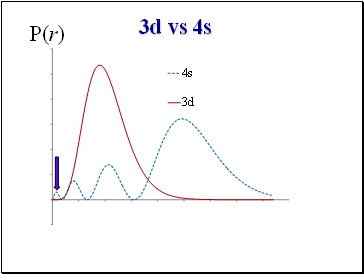
3d vs 4s

P(r)

Slide 46

The Angular Wavefunction

The Ylm(,) angular part

of the solution form a set

of functions called the

n.b. These are generally

imaginary functions -we use

real linear combinations to

picture them.

Slide 47

The Shapes of Wavefunctions (Orbitals)

Shapes arise from combination of radial R(r) and angular parts Ylm(,) of the wavefunction.

Usually represented as boundary surfaces which include of the probability density. The electron does not undergo planetary style circular orbits.