Atomic Structure and Periodic Trends

Page
7

(because the electron is bound)

iii) n= by definition has

energy zero, hence E- E1

= ionization energy (13.6 eV)

= Ry (109 677 cm-1)

Important

Slide 57

The Ionization Energy

Corresponds to the total removal of an electron (i.e., transition to n=)

Since in the ground state H-atom n=1 is the highest occupied atomic orbital, the ionization energy is given by:

Important

See later for Koopman’s theorem

Slide 58

Other Atoms

Slide 59

A) Other single electron atoms/ions (H-like atoms)

The ions He+, Li2+, Be3+, B4+, . etc. are said to be with the H-atom (same electron configuration).

Again ns, np, nd etc. levels are degenerate.

However the attractive Coulomb force is much bigger due to the Z+charge of the nuclei.

The energy levels are given by a similar expression to that for the H-atom with the inclusion of a :

Slide 60

Note that exponential function decays faster as Z

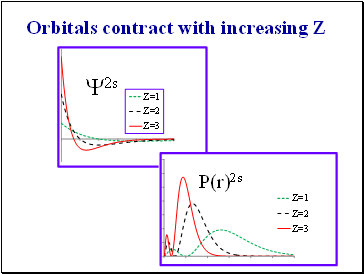
Orbitals contract with increasing Z

Slide 61

Orbitals contract with increasing Z

Y2s

Slide 62

H-like atoms/ions : Summary

The orbitals contract with increasing Z

The effect of the Z2 term is to increase the energy level spacing.

E.g., The energy level spacings in the He+ spectrum are approx. 4 times those in the H-atom whilst in Be3+ they are 16 times larger (Z=4).

This is only approximate because of the slight mass dependence of the Rydberg constant.

Ry(H) = 109 677cm-1 Ry(mass) = 109 737 cm-1

Compare ionisation energies for IE(H) = 13.6eV, IE(He+) = 54.4eV, IE(Li2+)=122.4eV

Slide 63

B) Multi-electron Atoms

Schrödinger equation cannot be solved analytically anymore (apart from He)

Need to develop an approximate picture for multi-electron atoms

2+

-

-

Helium atom

Slide 64

The orbital approximation in quantum mechanics

Y(r1, r2, …) = y(r1) y(r2)….

Total wavefunction of many electron atom

Each electron is occupying its individual orbital with nuclear charge modified to take account of all other electrons’ presence (repulsion!)

Slide 65

The orbital approximation in words