Atomic Structure and Periodic Trends

Page
12

p5

p6

s-block

p-block

Slide 99

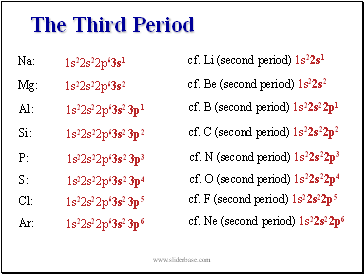
The Third Period

1s22s22p63s1

Na:

cf. Li (second period) 1s22s1

1s22s22p63s2

Mg:

cf. Be (second period) 1s22s2

1s22s22p63s2 3p1

Al:

cf. B (second period) 1s22s22p1

1s22s22p63s2 3p2

Si:

cf. C (second period) 1s22s22p2

1s22s22p63s2 3p3

P:

cf. N (second period) 1s22s22p3

1s22s22p63s2 3p4

S:

cf. O (second period) 1s22s22p4

1s22s22p63s2 3p5

Cl:

cf. F (second period) 1s22s22p5

1s22s22p63s2 3p6

Ar:

cf. Ne (second period) 1s22s22p6

Slide 100

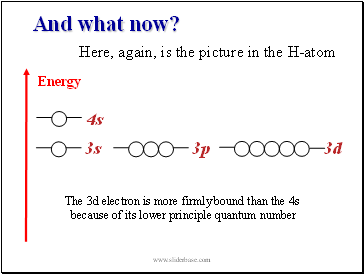
And what now?

3s

3p

3d

4s

Here, again, is the picture in the H-atom

The 3d electron is more firmly bound than the 4s

because of its lower principle quantum number

Energy

Slide 101

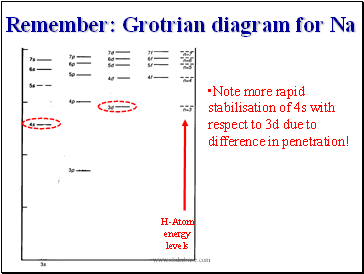
Remember: Grotrian diagram for Na

Note more rapid stabilisation of 4s with respect to 3d due to difference in penetration!

H-Atom

energy

levels

Slide 102

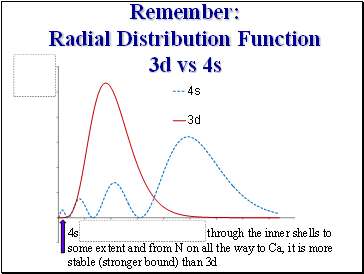
Remember:

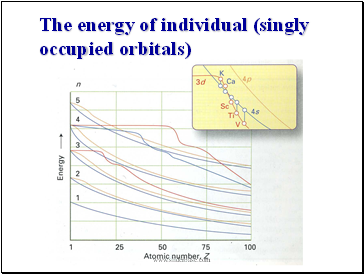
Radial Distribution Function 3d vs 4s

4s through the inner shells to some extent and from N on all the way to Ca, it is more stable (stronger bound) than 3d

Slide 103

The energy of individual (singly occupied orbitals)

Slide 104

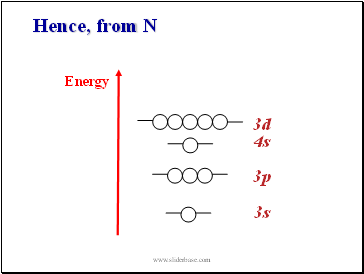
Hence, from N

3s

3p

3d

4s

Energy

Slide 105

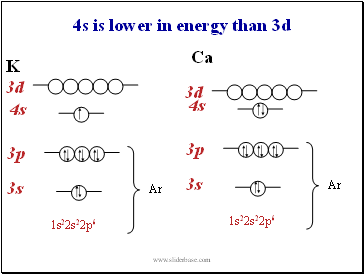
4s is lower in energy than 3d

3s

3p

3d

4s

Ar

1s22s22p6

K

Ca

3s

3p

3d

4s

Ar

1s22s22p6

Slide 106

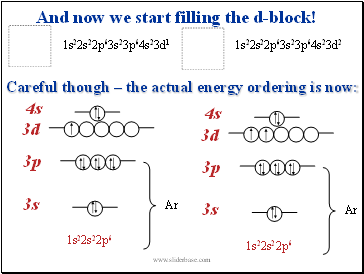
Careful though – the actual energy ordering is now:

3s

3p

3d

4s

Ar

1s22s22p6

3s

3p

3d

4s

Ar

1s22s22p6

1s22s22p63s23p64s23d1

1s22s22p63s23p64s23d2

And now we start filling the d-block!

Slide 107

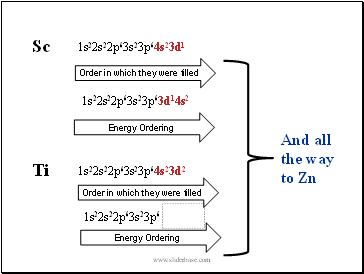
Sc

Ti

1s22s22p63s23p64s23d1

1s22s22p63s23p64s23d2

Order in which they were filled

Energy Ordering

And all the way to Zn

Order in which they were filled

1s22s22p63s23p6

Energy Ordering

1s22s22p63s23p63d14s2

Slide 108

Ti

1s22s22p63s23p63d24s2

Important for formation of ions!

Ti3+

1s22s22p63s23p63d24s2